EDP Sciences logo
Authentification abonné
Rechercher
Menu
Numéro
J. Phys. III France
Volume 2, Numéro 2, February 1992
Page(s) 203 - 212
DOI https://doi.org/10.1051/jp3:1992118
DOI: 10.1051/jp3:1992118
J. Phys. III France 2 (1992) 203-212

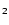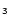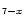Loi d'échelle dans YBa $\mathsf{_2}$Cu $\mathsf{_3}$O ${_{\mathsf{7}-x}}$ céramique

J. C. Soret and L. Ammor

Université de Tours, Laboratoire de Physique Electronique et Thermodynamique des Oxydes, U.F.R. Sciences, 37200 Tours, France.

(Reçu le 7 novembre 1990, révisé le 16 juillet 1991, accepté le 10 septembre 1991)

Abstract
Our measurements V- I in YBa 2Cu 3O 7-x ceramic, in the limit I=0, confirm a second-order phase transition at a critical temperature $T_{\rm c}(0)<T_{\rm cs}$ where $T_{\rm cs}$ is the critical temperature of the superconducting intragranular phase transition. As $I\neq 0$, we show the existence of a crossover temperature T*(I) depending on the value of the current I. For the temperatures $T\gg T^{*}(I)>T_{\rm c}(0),\ \sigma\sim\bar{t}^{-\gamma}$ with $\gamma\simeq 0.9$ and $\bar{t}=(T-T_{\rm c}(I))/T_{\rm c}(0)$ where $T_{\rm c}(I)$ corresponds to the critical temperature shift due to I. This conductivity critical behaviour is identical to the one observed as $T\rightarrow T_{\rm c}(0)^+$ and I=0. For the temperature range $T_{\rm c}(I)<T\ll T^{*}(I)<T_{\rm c}(0)$ $ \sigma\sim A(I)\bar{t}^{-\tilde{\gamma}}$ with $\tilde{\gamma}=1.3$ and $A(I)=I^{(\tilde{\gamma}-\gamma)/\phi}$.

Résumé
Nos mesures V- I sur YBa 2Cu 3O 7-x céramique, dans la limite I=0, confirment une transition de phase du second ordre à une température critique $T_{\rm c}(0)<T_{\rm cs}$ où $T_{\rm cs}$ est la température de condensation des grains. En présence d'un courant non nul la température de transition est déplacée à $T_{\rm c}(I)<T_{\rm c}(0)$. Nous montrons l'existence d'une température de crossover T*(I) dépendante du courant I. Pour les températures $T\gg T^{*}(I)>T_{\rm c}(0),\ \sigma\sim\bar{t}^{-\gamma}$ avec $\gamma\simeq$ 0,9 et $\bar{t}=(T-T_{\rm c}(I))/T_{\rm c}(0)$, ce comportement est identique à celui observé en l'absence de courant (I=0) lorsque $T\rightarrow T_{\rm c}(0)^+$. Pour les températures $T_{\rm c}(I)\lesssim T\ll T^{*}(I)<T_{\rm c}(0),\ \sigma\sim A(I)\bar{t}^{-\tilde{\gamma}}$ avec $\tilde{\gamma}=$ 1,3 et $A(I)=I^{(\tilde{\gamma}-\gamma)/\phi}$.



© Les Editions de Physique 1992